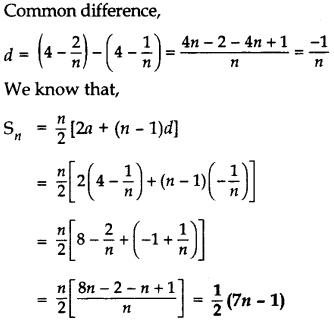• Maths Class 10th Arithmetic Progressions

  Chapters

10th Class - Mathematics

  Share

10th Class - Mathematics
  • Text Book Solutions
  • Important Question
  • Question Papers / Notes Download

Solutions

NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions

NCERT Solutions Exercise 5.1 Class 10 Arithmetic Progressions

Question 1.
In which of the following situations, does the list of numbers involved make an arithmetic progression and why?
  • (i) The taxi fare after each km when the fare is ₹ 15 for the first km and ₹ 8 for each additional km.
  • (ii) The amount of air present in a cylinder when a vacuum pump removes 14 of the air remaining in the cylinder at a time.
  • (iii) The cost of digging a well after every metre of digging, when it costs ₹ 150 for the first metre and rises by ₹ 50 for each subsequent metre.
  • (iv) The amount of money in the account every year, when ₹ 10000 is deposited at compound interest at 8% per annum.

Solution:
(i) Given:
a1 = ₹ 15
a2 = ₹ 15 + ₹ 8 = ₹ 23
a3 = ₹ 23 + ₹ 8 = ₹ 31
List of fares is ₹ 15, ₹ 23, ₹ 31
and a2 – a1 = ₹ 23 – ₹ 15 = ₹ 8
a3 – a2 = ₹ 31 – ₹ 23 = ₹ 8
Here, a2 – a1 = a3 – a2
Thus, the list of fares forms an AP.

(iii) Given:
a1 = ₹ 150, a2 = ₹ 200, a3 = ₹ 250
a2 – a1 = ₹ 200 – ₹ 150 = ₹ 50
and a3 – a2 = ₹ 250 – ₹ 200 = ₹ 50
Here, a3 – a2 = a2 – a1
Thus, the list forms an AP.
(iv) Given: a1 = ₹ 10000
a2 = ₹ 10000 + ₹ 10000 x 8/100 = ₹ 10000 + ₹ 800 = ₹ 10800
a3 = ₹ 10800 + ₹ 10800 x 8/100 = ₹ 10800 + ₹ 864 = ₹ 11664
a2 – a1 = ₹ 10800 – ₹ 10000 = ₹ 800
a3 – a2 = ₹ 11664 – ₹ 10800 = ₹ 864
a3 – a2 ≠ a2 – a1
Thus, it is not an AP.

Question 2.
Write first four terms of the AP, when the first term a and the common difference d are given as follows:
  • (i) a = 10, d = 10
  • (n) a = -2, d = 0
  • (iii) a = 4, d = -3
  • (iv) a = -1, d =1/2
  • (v) a = -1.25, d = -0.25
     

Solution:
(i) Given: a = 10, d = 10
a1 = 10,
a2 = 10 + 10 = 20
a3 = 20 + 10 = 30
a4 = 30 + 10 = 40
Thus, the first four terms of the AP are 10, 20, 30, 40.

(ii) Given: a = – 2, d = 0
The first four terms of the AP are -2, -2, -2, -2.

(iii) a1 = 4, d = -3
a2 = a1 + d = 4 – 3 = 1
a3 = a2 + d = 1 – 3 = -2
a4 = a3 + d = -2 – 3 = -5
Thus, the first four terms of the AP are 4, 1, -2, -5.

(iv)

(v) a1 = -1.25, d = -0.25
a2 = a1 + d = -1.25 – 0.25 = -1.50
a3 = a2 + d = -1.50 – 0.25 = -1.75
a4 = a3 + d = -1.75 – 0.25 = -2
Thus, the first four terms of the AP are -1.25, -1.50, -1.75, -2.

Question 3.
For the following APs, write the first term and the common difference:
  • (i) 3, 1, -1, -3, ……
  • (ii) -5, -1, 3, 7, ……
  • (iii)1/3,5/3,9/3,13/3, ……..
  • (iv) 0.6, 1.7, 2.8, 3.9, …….
     

Solution:
(i) a1= 3, a2 = 1
d = a2 - a1= 1 - 3 = -2
where, a1 = first term and d = common difference
a1 = 3, d = -2
(ii) a1= -5, a2= -1
d = a2 - a1= -1 - (-5) = -1 + 5 = 4
So, first term a1= -5 and common difference d = 4
(iii) a1=1/3, a2=5/3
d =5/3 - 1/3=4/3
So, first term a1=1/3 and common difference d =4/3
a1= 0.6, a2= 1.7
d = a2 - a1= 1.7 - 0.6 = 1.1
So, first term a1= 0.6 and common difference d = 1.1

Question 4.
Which of the following are APs ? If they form an AP, find the common difference d and write three more terms.
  • (i) 2, 4, 8, 16, …….
  • (ii) 2,5/2, 3,7/2, …….
  • (iii) -1.2, -3.2, -5.2, -7.2, ……
  • (iv) -10, -6, -2,2, …..
  • (v) 3, 3 + √2, 3 + 2√2, 3 + 3√2, …..
  • (vi) 0.2, 0.22, 0.222, 0.2222, ……
  • (vii) 0, -4, -8, -12, …..
  • (viii)−1/2, −1/2,−1/2,−1/2, …….
  • (ix) 1, 3, 9, 27, …….
  • (x) a, 2a, 3a, 4a, …….
  • (xi) a, a2, a3, a4, …….
  • (xii) √2, √8, √18, √32, …..
  • (xiii) √3, √6, √9, √12, …..
  • (xiv) 12, 32, 52, 72, ……
  • (xv) 12, 52, 72, 73, ……
     

Solution:
(i) 2, 4, 8, 16, ……
a2- a1 = 4 - 2 = 2
a3- a2 = 8 - 4 = 4
a2- a1 ≠ a3- a2
Thus, the given sequence is not an AP.

NCERT Solutions Exercise 5.2 Class 10 Arithmetic Progressions

Question 1.
Fill in the blanks in the following table, given that a is the first term, d the common difference and an the nth term of the AP:

Solution:

Question 2.
Choose the correct choice in the following and justify:
(i) 30th term of the AP: 10, 7, 4, …, is
  • (A) 97
  • (B) 77
  • (C) -77
  • (D) -87

(ii) 11th term of the AP: -3, −1/2, 2, …, is
(A) 28
(B) 22
(C) -38
(D) -48
 

Solution:
(i) 10, 7, 4, …,
a = 10, d = 7 – 10 = -3, n = 30
an = a + (n – 1)d
⇒ a30 = a + (30 – 1) d = a + 29 d = 10 + 29 (-3) = 10 – 87 = – 77
Hence, correct option is (C).

Question 3.
In the following APs, find the missing terms in the boxes:

Solution:

Question 4.
Which term of the AP: 3, 8, 13, 18, …, is 78?
 

Solution:
Given: 3, 8, 13, 18, ………,
a = 3, d = 8 – 3 = 5
Let nth term is 78
an= 78
a + (n - 1) d = 78
⇒ 3 + (n - 1) 5 = 78
⇒ (n - 1) 5 = 78 – 3
⇒ (n - 1) 5 = 75
⇒ n - 1 = 15
⇒ n = 15 + 1
⇒ n = 16
Hence, a16= 78

Question 5.
Find the number of terms in each of the following APs:

(i) 7, 13, 19, …, 205
(ii) 18, 15 1/2, 13, …, -47

Question 6.
Check, whether -150 is a term of the AP: 11, 8, 5, 2, ….
 

Solution:
11, 8, 5, 2, …….
Here, a = 11, d = 8 - 11= -3, an= -150
a + (n - 1) d = an
⇒ 11 + (n - 1) (- 3) = -150
⇒ (n - 1) (- 3) = -150 - 11
⇒ -3 (n - 1) = -161
⇒ n – 1 = −161−3
⇒ n =161/3 + 1 =164/3= 53 4/3
Which is not an integral number.
Hence, -150 is not a term of the AP.

Question 7.
Find the 31st term of an AP whose 11th term is 38 and the 16th term is 73.

a11 = 38 and a16 = 73
⇒ a11 = a + (11 - 1) d ⇒ a + 10d = 38 ….. (i)
⇒ a16 = a + (16 - 1 )d ⇒ a + 15d = 73 …(ii)
Subtracting eqn. (i) from (ii), we get
a + 15d - a - 10d = 73 - 38
⇒ 5d = 35
⇒ d = 1
From (i), a + 10 x 7 = 38
⇒ a = 38 - 70 = -32
a31= a + (31 - 1) d = a + 30d = -32 + 30 x 7 = - 32 + 210 = 178

Question 8.
An AP consists of 50 terms of which 3rd term is 12 and the last term is 106. Find the 29th term.
 

Solution:
Given:
a50 = 106
a50 = a + (50 – 1) d
⇒ a + 49d = 106 …(i)
and a3 = 12 ⇒ a3= a + (3 – 1 )d ⇒ a + 2d = 12 …(ii)
Subtracting eqn. (ii) from (i), we get
a + 49d - a -2d = 106 - 12
⇒ 47d = 94
⇒ d =94/47= 2
a + 2d = 12
⇒ a + 2 x 2 = 12
⇒ a + 4 = 12
⇒ a = 12 – 4 = 8
a29 = a + (29 - 1) d = a + 28d = 8 + 28 x 2 = 8 + 56 = 64

Question 9.
If the 3rd and the 9th term of an AP are 4 and -8 respectively, which term of this AP is zero?
 

Solution:
Given: a3= 4 and a9= -8
⇒ a3 = a + (3 - 1 )d ⇒ a + 2d = 4 …(i)
a9 = a + (9 - 1) d ⇒ a + 8d = -8 ….(ii)
Subtracting eqn. (i) from (ii), we get
a + 8d a - 2d = -8 - 4
⇒ 6d = -12.
⇒ d = -2
Now,
a + 2d = 4
⇒ a + 2(-2) = 4
⇒ a - 4 = 4
⇒ a = 4 + 4 = 8
Let an= 0
⇒ a + (n - 1) d = 0
⇒ 8 + (n - 1) (- 2) = 0
⇒ 8 = 2 (n - 1)
⇒ n - 1 = 4
⇒ n = 4 + 1 = 5
Hence, 5th term is zero.

Question 10.
The 17th term of an AP exceeds its 10th term by 7. Find the common difference.

Solution:
Given: a17 - a10= 7
⇒ [a + (17 - 1 ) d] - [a + (10 - 1 ) d] = 7
⇒ (a + 16d) - (a + 9d) = 7
⇒ 7d = 7
⇒ d = 1

 Question 11.
Which term of the AP: 3, 15, 27, 39, … will be 132 more than its 54th term?
 

Solution:
3, 15, 27, 39, …..
Here, a = 3, d = 15 – 3 = 12
Let an= 132 + a54
⇒ an- a54= 132
⇒ [a + (n - 1) d] - [a + (54 - 1) d] = 132
⇒ a + nd - d - a - 53d = 132
⇒ 12n - 54d = 132
⇒ 12n - 54 x 12 = 132
⇒ (n - 54)12 = 132
⇒ n - 54 = 11
⇒ n = 11 + 54 = 65

Question 12.
Two APs have the same common difference. The difference between their 100th terms is 100, what is the difference between their 1000th terms?
 

Solution:
Let a and A be the first term of two APs and d be the common difference.
Given:
a100- A100= 100
⇒ a + 99d - A - 99d = 100
⇒ a - A = 100
⇒ a1000 – A1000= a + 999d - A - 999d
⇒ a - A = 100
⇒ a1000- A1000= 100

Question 13.
How many three-digit numbers are divisible by 7?
 

Solution:
The three-digit numbers which are divisible by 7 are 105, 112, 119, ………., 994
Here, a = 105, d = 112 - 105 = 7 , an= 994
a + (n - 1) d = 994
⇒ 105 + (n - 1) 7 = 994
⇒ (n - 1) 7 = 994 - 105
⇒ 7 (n - 1) = 889
⇒ n - 1 = 127
⇒ n = 127 + 1 = 128

Question 14.
How many multiples of 4 lie between 10 and 250?
 

Solution:
The multiples of 4 between 10 and 250 be 12, 16, 20, 24,…., 248
Here, a = 12, d = 16 - 12 = 4, an= 248
an= a + (n - 1) d
⇒ 248 = 12 + (n - 1) 4
⇒ 248 - 12 = (n - 1) 4
⇒ 236 = (n - 1) 4
⇒ 59 = n - 1
⇒ n = 59 + 1 = 60

 Question 15.
For what value of n, the nth term of two APs: 63, 65, 61,… and 3, 10, 17,… are equal?
 

Solution:
First AP
63, 65, 67,…
Here, a = 63, d = 65 - 63 = 2
an= a + (n - 1) d = 63 + (n - 1) 2 = 63 + 2n - 2 = 61 + 2n
Second AP
3, 10, 17, …
Here, a = 3, d = 10 - 3 = 7
an= a + (n - 1) d = 3 + (n - 1)7 = 3 + 7n - 7 = 7n - 4
Now, an= an
⇒ 61 + 2n = 7n - 4
⇒ 61 + 4 = 7n - 2n
⇒ 65 = 5n
⇒ n = 13

Question 16.
Determine the AP whose 3rd term is 16 and 7th term exceeds the 5th term by 12.
 

Solution:
Given: a3 16
⇒ a + (3 - 1)d = 16
⇒ a + 2d = 16
and a7- a5= 12
⇒ [a + (7 - 1 )d] - [a + (5 - 1 )d] = 12
⇒ a + 6d - a - 4d = 12
⇒ 2d = 12
⇒ d = 6
Since a + 2d = 16
⇒ a + 2(6) = 16
⇒ a + 12 = 16
⇒ a = 16 - 12 = 4
a1= a = 4
a2= a1+ d = a + d = 4 + 6 = 10
a3= a2+ d = 10 + 6 = 16
a4= a3+ d = 16 + 6 = 22
Thus, the required AP is a1, a2, a3, a4,…, i.e. 4, 10, 16, 22

Question 17.
Find the 20th term from the last term of the AP: 3, 8, 13, …, 253.
 

Solution:
Given: AP is 3, 8, 13,…….. ,253
On reversing the given A.P., we have
253, 248, 243 ,………, 13, 8, 3.
Here, a = 253, d = 248 – 253 = -5
a20 = a + (20 – 1)d = a + 19d = 253 + 19 (-5) = 253 – 95 = 158

Question 18.
The sum of the 4th and 8th terms of an AP is 24 and the sum of the 6th and 10th terms is 44. Find the first three terms of the AP.
 

Solution:

Question 19.
Subba Rao started work in 1995 at an annual salary of ₹ 5000 and received an increment of ₹ 200 each year. In which year did his income reach ₹ 7000 ?
 

Solution:
a = ₹ 5000, d = ₹ 200
Let an= ₹ 7000
We have, a + (n - 1) d = 7000
⇒ 5000 + (n - 1) 200 = 7000
⇒ (n - 1) 200 = 7000 - 5000
⇒ (n - 1) 200 = 2000
⇒ (n- 1) = 10
⇒ n = 11
⇒ 1995 + 11 = 2006
Hence, in 2006 Subba Rao’s income will reach ₹ 7000.

Question 20.
Ramkali saved ₹ 5 in the first week of a year and then increased her weekly saving by ₹ 1.75. If in the nth week, her weekly saving become ₹ 20.75, find n.
 

Solution:
Given: a = ₹ 5, d = ₹ 1.75
an= ₹ 20.75
a + (n - 1) d - 20.75
⇒ 5 + (n - 1) 1.75 = 20.75
⇒ (n - 1) x 1.75 = 20.75 - 5
⇒ (n - 1) 1.75 = 15.75
⇒ n - 1 = 9
⇒ n = 9 + 1
⇒ n = 10
Hence, in 10th week Ramkali’s saving will be ₹ 20.75.

NCERT Solutions Exercise 5.3 Class 10 Arithmetic Progressions

Question 1.
Find the sum of the following APs:
  • (i) 2, 7, 12,…… to 10 terms.
  • (ii) -37, -33, -29, …… to 12 terms.
  • (iii) 0.6, 1.7, 2.8, ……, to 100 terms.
  • (iv)1/15,1/12,1/10, …….., to 11 terms.
     

Solution:

Question 2.
Find the sums given below:
  • (i) 7 + 10 1/2+ 14 + … + 84
  • (ii) 34 + 32 + 30 + … + 10
  • (iii) -5 + (-8) + (-11) + ….. + (-230)

Solution:

Question 3.
In an AP:
  • (i) given a = 5, d = 3, an= 50, find n and Sn.
  • (ii) given a = 7, a13= 35, find d and S13.
  • (iii) given a12= 37, d = 3, find a and S12.
  • (iv) given a3= -15, S10= 125, find d and a10.
  • (v) given d = 5, S9= 75, find a and a9.
  • (vi) given a = 2, d = 8, Sn= 90, find n and an.
  • (vii) given a = 8, an= 62, Sn= 210, find n and d.
  • (viii) given an= 4, d = 2, Sn= -14, find n and a.
  • (ix) given a = 3, n = 8, S = 192, find d.
  • (x) given l = 28, S = 144, and there are total 9 terms. Find a.
     

Solution:

Question 4.
How many terms of AP: 9, 17, 25, … must be taken to give a sum of 636?
 

Solution:

Question 5.
The first term of an AP is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference.
 

Solution:
 

Question 6.
The first and the last terms of an AP are 17 and 350 respectively. If the common difference is 9, how many terms are there and what is their sum?
 

Solution:

Question 7.
Find the sum of first 22 terms of an AP in which d = 7 and 22nd term is 149.
 

Solution:

Question 8.
Find the sum of first 51 terms of an AP whose second and third terms are 14 and 18 respectively.
 

Solution:

Question 9.
If the sum of first 7 terms of an AP is 49 and that of 17 terms is 289, find the sum of first n terms.
 

Solution:

Question 10.
Show that a1, a2, ……. an,…… form an AP where an is defined as below:

(i) an= 3 + 4n
(ii) an= 9 - 5n
Also find the sum of the first 15 terms in each case.
 

Solution:

Question 11.
If the sum of the first n terms of an AP is 4n - n2, what is the first term (that is S1)? What is the sum of first two terms? What is the second term? Similarly, find the 3rd, the 10th and the nth terms.
 

Solution:

Question 12.
Find the sum of the first 40 positive integers divisible by 6.
 

Solution:

Question 13.
Find the sum of the first 15 multiples of 8.
 

Solution:

Question 14.
Find the sum of the odd numbers between 0 and 50.
 

Solution:
Let odd numbers between 0 and 50 be 1, 3, 5, 7,…….., 49.

Question 15.
A contract on construction job specifies a penalty for delay of completion beyond a certain date as follows:
₹ 200 for the first day, ₹ 250 for the second day, ₹ 300 for the third day, etc. the penalty for each succeeding day being ₹ 50 more than for the preceding day. How much money the contractor has to pay as penalty, if he has delayed the work by 30 days?
 

Solution:

Question 16.
A sum of ₹ 700 is to be used to give seven cash prizes to students of a school for their overall academic performance. If each prize is ₹ 20 less than its preceding prize, find the value of each of the prizes.
 

Solution:
Let 1st prize be of ₹ a
2nd prize be ₹ (a - 20) and
3rd prize be ₹ (a - 20 - 20) = ₹ (a - 40)

Question 17.
In a school, students thought of planting trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be the same as the class, in which they are studying, eg. a section of Class I will plant 1 tree, a section of Class II will plant 2 trees and so on till Class XII. There are three sections of each class. How many trees will be planted by the students?
 

Solution:
Let the trees be planted 1, 2, 3, 4, 5 , …… 12
Here, a = 1, d = 1, n = 12
Total number of trees planted by each section
S12=122[2a + (n - 1) d] = 6 [2 x 1 + (12 - 1) x 1]
= 6 [2 + 11] = 6 x 13 = 78
Total number of trees planted by 3 sections = 78 x 3 = 234

Question 18.
A spiral is made up of successive semicircles, with centres alternately at A and B, starting with centre at A, of radii 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm,… as shown in figure. What is the total length of such a spiral made up of thirteen consecutive semicircles?
(Take π =22/7)
[Hint:Length of successive semicircles is l1, l2, l3, l4, … with centres at A, B, respectively.]

Solution:

Question 19.
200 logs are stacked in the following manner 20 logs in the bottom row, 19 in the next row, 18 in the row next to it and so on (see Figure). In how many rows are the 200 logs placed and how many logs are in the top row?

Solution:

Question 20.
In a potato race, a bucket is placed at the starting point, which is 5 m from the first potato, and the other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line (see Fig.) A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are in the bucket. What is the total distance the competitor has to run?
[Hint: To pick up the first potato and the second potato, the total distance (in metres) run by a competitor is 2 x 5 + 2 x (5 + 3)]

Solution:
Distance between the first potato and the bucket = 5 m
Distance between next 2 potatoes = 3 m each
So, series is 5 m, 8 m, 11 m,
Here, a = 5 m, d = (8 - 5) m = 3 m
Total distance travelled for 10 potatoes = 2 [5 + 8 + 11 + …….. + 10 terms]
= 2[102{2 x 5 + (10 - 1) 3}]
= 2[5{10 + 27}] = 2(37 x 5) = 37 x 10 = 370 m.

NCERT Solutions Exercise 5.4 Class 10 Arithmetic Progressions

Question 1.
Which term of the AP: 121, 117. 113, ….., is its first negative term?
 

Solution:
 

Question 2.
The sum of the third term and the seventh term of an AP is 6 and their product is 8. Fibd the sum of first sixteen terms of the AP?
 

Solution:

Question 3.
A ladder has rungs 25 cm apart. The rungs decrease uniformly in length from 45 cm at the bottom to 25 at the top. If the top and the bottom rungs are 2 1/2 m apart, what is the length of the wood required for the rungs?

Solution:

Question 4.
The houses of a row are numbered consecutively from 1 to 49. Show that there is value of x such that the sum of the numbers of the houses preceding the house numbered x is equal to the sum of the numbers of the houses following it. Find this value of x.
 

Solution:
 

Question 5.
A small terrace at a football ground comprises of 15 steps each of which is 50 m long and built of solid concrete. Each step has a rise of 1/2 m and a tread of 1/2 m. Calculate the total volume of concrete required to build the terrace.

Solution:

Important Question

NCERT CBSE for Class 10 Maths Chapter 5 Arithmetic Progressions Important Questions

Arithmetic Progressions Class 10 Important Questions Very Short Answer (1 Mark)

Question 1.
Find the common difference of the AP 1/p,1-p/p,1-2p/p,..
Year of Question:(2013D)

Solution:
The common difference,

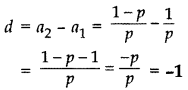
Question 2.
Find the common difference of the A.P. 1/2b,1-6b/2b,1-12b/2b,..
Year of Question:(2013D)

Solution:
The common difference, d = a2- a1 = 1-6b/2b - 1/2b
= 1-6b-1/2b = -6b/2b = -3

Question 3.
Find the common difference of the A.P. 1/3q,1-6q/3q,1-12q/3q,..
Year of Question:(2013D)

Solution:
The common difference, d = a2- a1 = 1-6q/3q - 1/3q
= 1-6q-1/3q = -6q/3q = -2

Question 4.
Calculate the common difference of the A.P. 1/b,3-b/3b,3-2b/3b,..
Year of Question:(2013D)

Solution:
Common difference, d = a2 - a1= 3-b/3b-1/b
= 3-b-3/3b=-b/3b=-1/3

Question 5.
Calculate the common difference of the A.P. 1/3,1-3b/3,1-6b/3,.
Year of Question:(2013OD)

Solution:
Common difference, d = a2 - a1 = 1-3b/3 - 1/3
= 1-3b-1/3=-3b/3 = -b

Question 6.
What is the common difference of an A.P. in which a21 - a7 = 84?
Year of Question:(2017OD)

Solution:
a21 - a7 = 84 .[Given
∴ (a + 20d) - (a + 6d) = 84 .[an = a + (n - 1)d
20d - 6d = 84
14d = 84 ⇒ d 84/14 = 6

Question 7.
Find the 9th term from the end (towards the first term) of the A.P. 5,9,13, ., 185.
Year of Question:(2016D)

Solution:
Here First term, a = 5
Common difference, d = 9 - 5 = 4
Last term, 1 = 185
nth term from the end = l - (n - 1)d
9th term from the end = 185 - (9 - 1)4
= 185 - 8 × 4 = 185 - 32 = 153

Arithmetic Progressions Class 10 Important Questions Short Answer-I (2 Marks)

Question 8.
The angles of a triangle are in A.P., the least being half the greatest. Find the angles.
Year of Question:(2011D)

Solution:
Let the angles be a - d, a, a + d; a > 0, d > 0
∵Sum of angles = 180°
∴ a - d + a + a + d = 180°
⇒ 3a = 180° ∴ a = 60° .(i)
By the given condition
a - d = a+d/2
⇒ 2 = 2a - 2d = a + d
⇒ 2a - a = d + 2d ⇒ a = 3d
⇒ d = a/3=60°/3 = 20° . [From (i)
∴ Angles are: 60° - 20°, 60°, 60° + 20°
i.e., 40°, 60°, 80°

Question 9.
Find whether -150 is a term of the A.P. 17, 12, 7, 2, . ?
Year of Question:(2011D)

Solution:
Given: 1st term, a = 17
Common difference, d = 12 - 17 = -5
nth term, an = - 150 (Let)
∴ a + (n - 1) d = - 150
17 + (n - 1)(-5) = - 150
(n - 1) (-5) = - 150 - 17 = - 167
(n ? 1) = -167/-5
n = 167/5 + 1 = 167+5/5=172/5
n = 172/5 .[Being not a natural number
∴ -150 is not a term of given A.P.

Question 10.
Which term of the progression 4, 9, 14, 19, . is 109?
Year of Question:(2011D)

Solution:
Here, d = 9 -4 = 14 -9 = 19 - 14 = 5
∴ Difference between consecutive terms is constant.
Hence it is an A.P.
Given: First term, a = 4, d = 5, an = 109 (Let)
∴ an = a + (n - 1) d . [General term of A.P.
∴ 109 = 4 + (n - 1) 5
⇒ 109 - 4 = (n - 1) 5
⇒ 105 = 5(n ? 1) ⇒ n - 1 = 105/5 = 21
⇒ n = 21 + 1 = 22 ∴ 109 is the 22nd term

Question 11.
Which term of the progression 20, 192, 183, 17 . is the first negative term?
Year of Question:(2017OD)

Solution:
Given: A.P.: 20, 77/4,37/4,71/4
Here a = 20, d = 77-80/4=-3/4
For first negative term, an < 0
⇒ a + (n - 1)d < 0 ⇒ 20 + (n - 1)(- 3/4) < 0
⇒ - 3/4(n - 1) < -20 ⇒ 3(1 - 1) > 80
⇒ 3n - 3 > 80 ⇒ 3n > 83
n > 83/4 ⇒ n > 27.5
∴ Its negative term is 28th term.

Question 12.
The 4th term of an A.P. is zero. Prove that the 25th term of the A.P. is three times its 11th term.
Year of Question:(2016OD)

Solution:
Let 1st term = a, Common difference = d
a4 = 0 a + 3d = 0 ⇒ a = -3d . (i)
To prove: a25 = 3 × a11
a + 24d = 3(a + 10d) .[From (i)
⇒ -3d + 24d = 3(-3d + 10d)
⇒ 21d = 21d
From above, a25 = 3(a11) (Hence proved)

Question 13.
The 7th term of an A.P. is 20 and its 13th term is 32. Find the A.P.
Year of Question:(2012OD)

Solution:
Let a be the 1th term and d be the common difference.

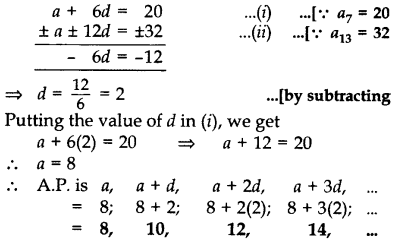
Question 14.
Find 10th term from end of the A.P. 4,9, 14, ., 254.
Year of Question:(2011OD)

Solution:
Common difference d = 9 - 4
= 14 - 9 = 5
Given: Last term, l = 254, n = 10
nth term from the end = l - (n - 1) d
∴ 10th term from the end = 254 - (10 - 1) × 5
= 254 - 45 = 209

Question 15.
Find how many two-digit numbers are divisible by 6?
Year of Question:(2011OD)

Solution:
12, 18, 24, .,96
Here, a = 12, d = 18 - 12 = 6, an = 96
a + (n - 1)d = an
∴ 12 + (n - 1)6 = 96
⇒ (n ? 1)6 = 96 - 12 = 84
⇒ n - 1 = 84/6 = 14
⇒ n = 14 + 1 = 15
∴ There are 15 two-digit numbers divisible by 6.

Question 16.
How many natural numbers are there between 200 and 500, which are divisible by 7?
Year of Question:(2011OD)

Solution:
203, 210, 217, ., 497
Here a = 203, d = 210 - 203 = 7, an = 497
∴ a + (n - 1) d = an
203 + (n - 1) 7 = 497
(n - 1) 7 = 497 - 203 = 294
n - 1 = 294/7 = 42 ∴ n = 42 + 1 = 43
∴ There are 43 natural nos. between 200 and 500 which are divisible by 7.

Question 17.
How many two-digit numbers are divisible by 3?
Year of Question:(2012OD)

Solution:
Two-digit numbers divisible by 3 are:
12, 15, 18, ., 99
Here, a = 12, d = 15 - 12 = 3, an = 99
∴ a + (n - 1)d = an
12 + (n - 1) (3) = 99
(n - 1) (3) = 99 -12 = 87
n - 1 = 87/3 = 29
∴ n = 29 + 1 = 30
∴ There are 30 such numbers.

Question 18.
How many three-digit natural numbers are divisible by 7?
Year of Question:(2013D)
Solution:
"3 digits nos." are 100, 101, 102, ., 999
3 digits nos. "divisible by 7" are:
105, 112, 119, 126, ., 994
a = 105, d = 7, an = 994, n = ?
As a + (n - 1)d = 994 = an
∴ 105 + (n - 1)7 = 994
(n ? 1)7 = 994 - 105
(n - 1) = 889/7 = 127
∴ n = 127 + 1 = 128

Question 19.
Find the number of all three-digit natural numbers which are divisible by 9.
Year of Question:(2013OD)

Solution:
To find: Number of terms of A.P., i.e., n.
A.P. = 108 + 117 + 126 + . + 999
1st term, a = 108
Common difference, d = 117 - 108 = 9
an = 999
a + (n - 1)d = an
∴ 108 + (n - 1) 9 = 999
⇒ (n - 1) 9 = 999 - 108 = 891
⇒ (n - 1) = 891/9 = 99
∴n = 99 + 1 = 100

Question 20.
Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5.
Year of Question:(2014OD)

Solution:
Numbers divisible by both 2 and 5 are 110, 120, 130, ., 990.
Here a = 110, d = 120 - 110 = 10, an = 990
As a + (n - 1)d = an= 990
110 + (n - 1)(10) = 990
(n - 1)(10) = 990 - 110 = 880
(n - 1) = 294/7 = 88
∴ n = 88 + 1 = 89

Question 21.
Find the middle term of the A.P. 6, 13, 20, ., 216.
Year of Question:(2015D)

Solution:
The given A.P. is 6, 13, 20, ., 216
Let n be the number of terms, d = 7, a = 6, an = 216
an = a + (n - 1)d
∴ 216 = 6 + (n - 1).7
216 - 6 = (n - 1)7
2107 = n - 1 ⇒ 30 + 1 = n
⇒ n = 31
Middle term = (n+1/2)th term
= (31+1/2)=(32/2) = 16th term of the A.P.
∴ a16 = a + 15d = 6 + 15 × 7 = 111

Question 22.
Find the middle term of the A.P. 213, 205, 197, . 37.
Year of Question:(2015D)
Solution:
A.P. : 213, 205, 197, ..... 37.
Let a and d be the first term and common difference of A.P. respectively,
Here a = 213, d = -8, an = 37, where n is the number of terms.
an = a + (n - 1)d
∴ 37 = 213 + (n - 1) (-8)
-176/-8 = n - 1 ⇒ n = 23
∴ Middle term = (n+1/2)th =(23+1/2)
= 12th term
∴ a12 = a + 11(d) = 213 + 11(-8) = 125

Question 23.
How many terms of the A.P. 27, 24, 21, . should be taken so that their sum is zero?
Year of Question:(2016D)

Solution:
Here, 1st term, a = 27
Common difference, d = 24 - 27 = -3
Given: Sn = 0
⇒ n/2[2a + (n - 1)d] = 0
⇒ n/2[2(27) + (n - 1)(-3)] = 0
⇒ n(54 - 3n + 3) = 0
⇒ n(57 - 3n) = 0
⇒ n = 0 or (57 - 3n) = 0
⇒ -3n = -57
⇒ n = 19
Since n, i.e., number of terms cannot be zero.
∴ Number of terms = 19

Question 24.
How many terms of the A.P. 65, 60, 55, . be taken so that their sum is zero?
Year of Question:(2016D)

Solution:
1st term, a = 65
Common difference, d = 60 - 65 = -5
Sn = 0 .[Given
⇒ n/2[2a + (n - 1)d] = 0
⇒ n/2[2(65) + (n - 1)(-5)] = 0
⇒ n(130 - 5n + 5) = 0
⇒ n(135 - 5n) = 0
⇒ n = 0 or 135 - 5n = 0
-5n = -135
⇒ n = 27
Since n, i.e., number of terms can not be zero.
∴ Number of terms = 27

Question 25.
Find the sum of the first 25 terms of an A.P. whose nth term is given by tn = 2 - 3n.
Year of Question:(2012D)

Solution:
Given: tn = 2 - 3n
When n = 1, t1 = 2 - 3(1) = -1 ..(i)
When n = 25, t25 = 2 - 3(25) = -73 .(ii)
As Sn= n/2[t1 + tn], n = 25
∴ S25 = 25/2[-1 + (-73)] .. [From (1) and (ii)
= 25×(-74)/2 = 25 × (-37) = -925

Question 26.
The first and the last terms of an AP are 5 and 45 respectively. If the sum of all its terms is 400, find its common difference.
Year of Question:(2014D)

Solution:
Here, an = 45, Sn = 400, a = 5, n = ?, d = ?

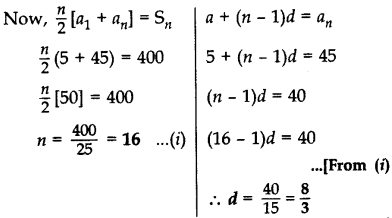
Question 27.
The first and the last terms of an AP are 8 and 65 respectively. If the sum of all its terms is 730, find its common difference.
Year of Question:(2014D)

Solution:
Here a, = a = 8; an = 65
Given: Sn = 730
⇒ n/2(8 + 65) = 730 ...[Sn = n/2(a1 + an)
n/2(73) = 730
n = 730 × 2/73 = 20
Now, an = a + (n ? 1)d = 65
8 +(20 - 1)d = 65 ⇒ 19d = 65 - 8 = 57
∴ d = 3

Question 28.
In an AP, if S5 + S7 = 167 and S10 = 235, then find the AP, where s, denotes the sum of its first n terms.
Year of Question:(2015OD)

Solution:
Given: S5 + S7 = 167
⇒ 5/2[2a + (5 - 1)d] + 7/2 [2a + (7 - 1)d] = 167 . [S<sub<n = n/2 (2a + (n - 1)d)
⇒ 5/2[2a + 4d] + 7/2[2a + 6d] = 167
⇒ 5(a + 2d) + 7(a + 3d) = 167
⇒ 5a + 10d + 7a + 210 = 167
⇒ 12a + 31d = 167
Now, S10 = 10/2 (2a + (10 - 1)d) = 235
⇒ 5[2a + 9d] = 235
⇒ 10a + 45d = 235
Solving (i) and (ii), we get a = 1 and d = 5
a1 = 1
a2 = a + d ⇒ 1 + 5 = 6
a3 = a + 2d ⇒ 1 + 10 = 11
Hence A.P. is 1, 6, 11.

Question 29.
Find the sum of all three digit natural numbers, which are multiples of 11.
Year of Question:(2012D)

Solution:
To find: 110 + 121 + 132 + . + 990
Here a = 110, d = 121- 110 = 11, an = 990
∴ a + (n - 1)d = 990
110 + (n - 1).11 = 990
(n - 1). 11 = 990 - 110 = 880
(n - 1) = 880 = 80
n = 80 + 1 = 81
As Sn = n/2 (a1 + an)
∴ S81 = 81/2 (110 + 990)
= 81/2 (1100) = 81 × 550 = 44,550

Arithmetic Progressions Class 10 Important Questions Short Answer - II (3 Marks)

Question 30.
Which term of the A.P. 3, 14, 25, 36, . will be 99 more than its 25th term?
Year of Question:(2011OD)

Solution:
Let the required term be nth term, i.e., an
Here, d = 14 - 3 = 11, a = 3
According to the Question, an = 99 + a25
∴ a + (n - 1) d = 99 + a + 24d
⇒ (n - 1) (11) = 99 + 24 (11)
(n - 1) (11) = 11 (9 + 24)
n - 1 = 33
n = 33 + 1 = 34
∴ 34th term is 99 more than its 25th term.

Question 31.
Determine the A.P. whose fourth term is 18 and the difference of the ninth term from the fifteenth term is 30.
Year of Question:(2011D)

Solution:

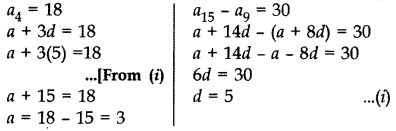
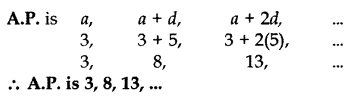
Question 32.
The 19th term of an AP is equal to three times its 6th term. If its 9th term is 19, find the A.P.
Year of Question:(2013OD)

Solution:
Given: a19 = 3(a6)
⇒ a + 18d = 3(a + 5d)
a + 18d = 3a + 15d
18d - 15d = 3a - a

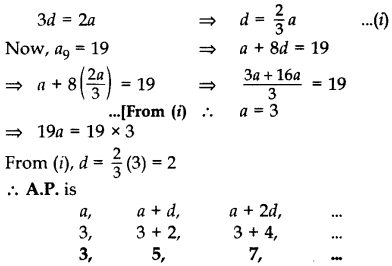
Question 33.
The 9th term of an A.P. is equal to 6 times its second term. If its 5th term is 22, find the A.P.
Year of Question:(2013OD)

Solution:
9th term = 6 (2nd term)
∴ a +8d = 6 (a + d) .[As an= a + (n - 1)d
a + 8d = 6a + 6d
8d - 6d = 6a - a
2d = 5a
⇒ d = 5a/2 .(i)
Now, a5 = 22
a + 4d = 22

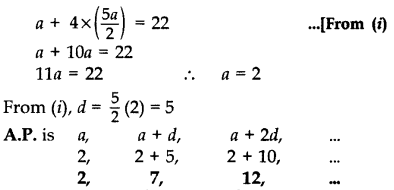
Question 34.
The sum of the 5th and the 9th terms of an AP is 30. If its 25th term is three times its 8th term, find the AP.
Year of Question:(2014OD)

Solution:
a5 + a9 = 30 . [Given
a + 4d + a + 8d = 30 .[∵ an = a + (n - 1)d
2a + 12d = 30 ⇒ a + 6d = 15 .[Dividing by 2
a = 15 - 6d .(i)
Now, a52 = 3(a8)
a + 24d = 3(a + 7d)
15 - 6d + 240 = 3(15 - 6d + 7d) .[From (i)
15 + 18d = 3(15 + d)
15 + 18d = 45 + 3d
18d - 3d = 45 - 15
15d = 30 ∴ d = 30/15 = 2
From (i), a = 15 - 6(2) = 15 - 12 = 3

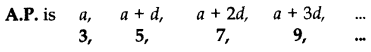
Question 35.
If the seventh term of an AP is 19 and its ninth term is 17, find its 63rd term.
Year of Question:(2014D)

Solution:

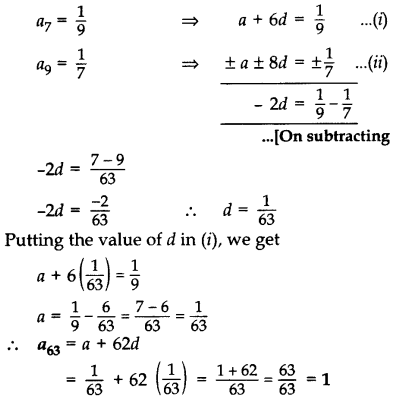
Question 36.
Find the value of the middle term of the following A.P.: -6, -2, 2, ., 58.
Year of Question:(2011D)

Solution:
Here a = -6, d = -2 -(-6) = 4, an = 58
As we know, a + (n - 1) d = 58
∴ -6 + (n - 1) 4 = 58
⇒ (n - 1) 4 = 58 + 6 = 64
⇒ (n - 1) = 64/4 = 16
⇒ n = 16 + 1 = 17 (odd)
Middle term = (n+1/2)th term
(17+1/2)th term = 9th term
∴ a9 = a + 8d = -6 + 8 (4) = -6 + 32 = 26
∴ Middle term = 26

Question 37.
Find the number of terms of the AP 18, 151/2, 13,., -491/2 and find the sum of all its terms.
Year of Question:(2014D)
Solution:
Here 1st term, a = 18
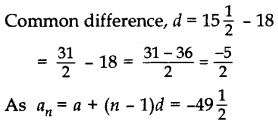
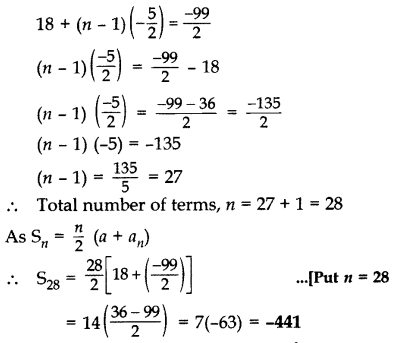
Question 38.
The 14th term of an AP is twice its gth term. If its 6th term is -8, then find the sum of its first 20 terms.
Year of Question:(2015OD)

Solution:
Let a = First term, d = Common difference
a14 = 2.a8 . [Given
⇒ a + 13d = 2 (a + 7d) ..[∵ a, = a + (n - 1)d
⇒ a + 13d = 2a + 14d
⇒ 1a - 2a = 14d - 13d
⇒ -1a = d ⇒ a = -d . (i)
a6 = -8 .[Given
⇒ -8 = a + 5d
⇒ -d + 5d = -8 .[From (i)
⇒ 4d = -8 ⇒ d = -2
Value of d put in equation (i), we get
a = -d ⇒ a=-(-2)
Now, a = 2, d = -2
Now, Sum of first 20 terms,
S20 = 20/2[2 × 2 + (20 - 1)(-2)] .[Sn = n/2 (2a + (n - 1)d)
S20 = 10[4 + 19(-2)]
S20 = 10[4 - 38] = -340

Question 39.
The 13th term of an AP is four times its 3rd term. If its fifth term is 16, then find the sum of its first ten terms.
Year of Question:(2015OD)

Solution:
a13 = 4a3 . [Given
⇒ a + 12d = 4(a + 2d) .[∵ an = a + (n - 1)d
⇒ a + 12d - 4a - 8d = 0
⇒ 4d = 3a ⇒ d = 3a/4 .(i)
a5 = 16 . [Given
⇒ a + 4d = 16
⇒ a +4(3a/4) = 16 . [From (i)
⇒ a + 3a = 16
⇒ 4a = 16 ⇒ a = 16/4 = 4 ..(ii)
Putting a = 4 in (i), we get a = 3
⇒ d = 3×4/4 = 3 . [From (ii)
∴ Sn = n/2 [2a + (n - 1)d]
S10 = 10/2 [2(4) + (10 - 1)(3)] .[n = 10 (Given)
S10 = 5 (8 + 27) ⇒ 5(35) = 175

Question 40.
If the sum of first 7 terms of an A.P is 49 and that of its first 17 terms is 289, find the sum of first n terms of the A.P.
Year of Question:(2016D)

Solution:
Let 1st term = a, Common difference = d
Given: S7 = 49, S17 = 289

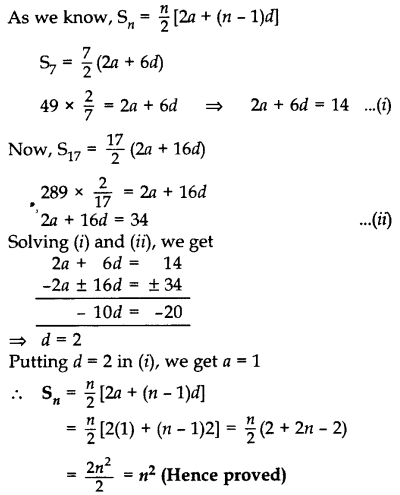
Question 41.
The first term of an A.P. is 5, the last term is 45 and the sum of all its terms is 400. Find the number of terms and the common difference of the A.P.
Year of Question:(2017OD)

Solution:
First term, a = 5, Last term, an = 45
Let the number of terms = n
Sn = 400
n/2 (a + an) = 400
n/2(5 + 45) = 400
n/2 (50) = 400
n = 400/25 = 16 = Number of terms
Now, an = 45
a + (n - 1)d = an
5+ (16 - 1)d = 45
15d = 45 - 5 ∴d = 40/15=8/3

Question 42.
The nth term of an A.P. is given by (-4n + 15). Find the sum of first 20 terms of this A.P.
Year of Question:(2013D)

Solution:
We have, an = -4n + 15
Put n = 1, a1 = -4(1) + 15 = 11
Put n=2, a2 = -4(2) + 15 = 7
∴ d = a2 - a1 = 7 - 11 = -4
As Sn = n/2 (2a + (n - 1)d]
∴ S20 = 20/2 [2(11) + (20 - 1)(-4)). [n = 20 (Given)
= 10 (22 - 76)
= 10 (-54) = -540

Question 43.
The sum of first n terms of an AP is 3n2 + 4n. Find the 25th term of this AP.
Year of Question:(2013D)

Solution:
We have, Sn = 3n2 + 4n
Put n = 25,
S25 = 3(25)2 + 4(25)
= 3(625) + 100
= 1875 + 100 = 1975
Put n = 24,
S24 = 3(24)2 + 4(24)
= 3(576) + 96
= 1728 + 96 = 1824
∴ 25th term = S25 - S24
= 1975 - 1824 = 151

Question 44.
The sum of the first seven terms of an AP is 182. If its 4th and the 17th terms are in the ratio 1 : 5, find the AP.
Year of Question:(2014OD)

Solution:
S7 = 182 .[Given

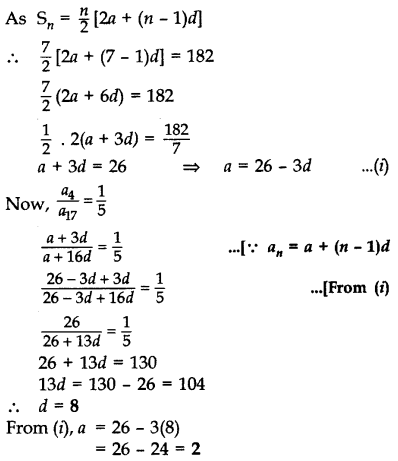
∴ a = 2, d = 8
∴AP is 2, 10, 18, 26, 34, .

Question 45.
If Sn, denotes the sum of first n terms of an A.P., prove that S12 = 3(S8 - S4).
Year of Question:(2015D)

Solution:
Let a be the first term and d be the common difference of A.P.
Sn = n/2 (2a + (n - 1)d)
∴ S12 = 12/2 (2a + (12 - 1)d)
S12 = 6 [2a + 11d] = 124 + 66d .(i)
∴ S8 = 8n/2 (2a + (8 - 1)d)
S8 = 4[2a + 7d] = 8a + 28d . (ii)
∴ S4 = 4/2 (2a + (4 - 1)d)
S4 = 2[2a + 3d) = 4a + 6d .(iii)
Now, S12 = 3(S8 - S4)
12a + 660 = 3(8a + 28d - 4a - 6d) . [From (i), (ii) & (iii)
12a + 660 = 3(4a + 22d)
12a + 660 = 12a + 66d .Hence proved

Question 46.
If the sum of the first n terms of an A.P. is 12 (3n2 + 7n), then find its nth term. Hence write its 20th
Year of Question:(2015D)

Solution:
Sn = 1/2 (3n2 + 7n) .[Given
Put n = 1
S1 = 1/2[3(1)2 + 7(1)] = 1/2 [3 + 7) = 1/2 (10) = 5
Put n = 2
S2 = 1/2 [3(2)2 + 7(2)] = 1/2[3(4) + 7(2)]
= S2 = 1/2(12 + 14) = 1/2 (26) = 13
Now we know,
S1 = 27 and a2 = S2 - S1
∴ a1 = 5 = 13 - 5 = 8
Now we have,
a1 = 5, a2 = 8, d = a2 - a1 = 8 - 5 = 3
an = a + (n - 1)d = 5 + (n - 1)3
= 5 + 3n - 3 = 3n + 2 (nth term)
∴ 20th term, a20 = (3 × 20) + 2 = 62

Question 47.
If Sn denotes the sum of first n terms of an A.P., prove that S30 = 3[S20 - S10].
Year of Question:(2015D)

Solution:
Let a be the first term and d be the common difference of the A.P.
Sn = n/2[2a + (n - 1)d]
S30 = 30/2 [2a + (30 - 1)d] = 15[2a + 29d]
= 30a + 435d .(i)
S20 = 20/2 [2a + (20 - 1)d] = 10[2a + 19d]
= 20a + 190d .(ii)
S10 = 10/2[2a + (10 - 1)d] = 5[2a + 9d]
= 10a + 45d .(iii)
To prove, 3(S20 - S10) = S30
= 3(20a + 190d - 10a - 45d) .[From (i), (ii) & (iii)
= 3(10a + 145d)
= 30a + 435d = S30 .Hence Proved

Question 48.
If the ratio of the sum of first n terms of two A.Ps is (7n + 1): (4n + 27), find the ratio of their mth terms.
Year of Question:(2016OD)

Solution:
Let A be first term and D be the common difference of 1st A.P.
Let a be the first term and d be the common difference of 2nd A.P.

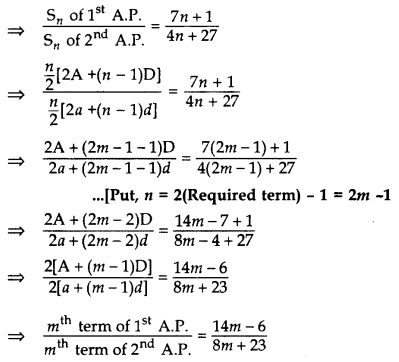
∴ Required ratio = (14m - 6) : (8m + 23)

Question 49.
The digits of a positive number of three digits are in A.P. and their sum is 15. The number obtained by reversing the digits is 594 less than the original number. Find the number.
Year of Question:(2016OD)

Solution:
Let hundred’s place digit = (a - d)
Let ten’s place digit = a
Let unit’s place digit = a + d
According to the Question,
a - d + a + a + d = 15
⇒ 3a = 15 ⇒ a = 5
Original number
= 100(a - d) + 10(a) + 1(a + d)
= 100a - 100d + 10a + a + d
= 111a - 99d
Reversed number
= 1(a - d) + 10a + 100(a + d)
= a - d + 10a + 100a + 100d
= 111a + 99d
Now, Original no. - Reversed no. = 594
111a - 99d - (111a + 99d) = 594
-198d = 594 ⇒ d = 594/-198 = -3
∴ The Original no. = 111a - 99d
= 111(5) - 99(-3)
= 555 + 297 = 852

Question 50.
The sums of first n terms of three arithmetic progressions are S1 S2 and S3 respectively. The first term of each A.P. is 1 and their common differences are 1, 2 and 3 respectively. Prove that S1 + S3 = 2S2.
Year of Question:(2016OD)

Solution:

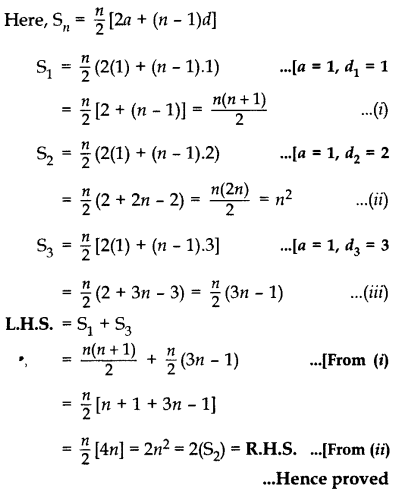
Question 51.
Find the sum of all three digit natural numbers, which are multiples of 9.
Year of Question:(2012D)

Solution:
To find: 108 + 117 + 126 + . + 999
1st term, a = 108
Common difference, d = 117 - 108 = 9
∴ a + (n - 1)d = an = 999
108 + (n - 1). 9 = 999
(n - 1)9 = 999 - 108 = 891
(n - 1) = 891/9 = 99
n = 99 + 1 = 100
As Sn= n/2(a1 + an)
∴ S100 = [latex]100/2[/latex] (108 + 999)
= 50(1107) = 55350

Question 52.
Find the sum of all multiples of 7 lying between 500 and 900.
Year of Question:(2012OD)

Solution:
To find: 504 + 511 + 518 + . + 896
a = 504, d = 511- 504 = 7, an = 896
a + (n - 1)d = an
∴ 504 + (n - 1)7 = 896
(n - 1)7 = 896 - 504 = 392

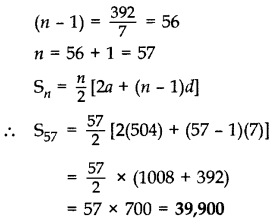
Arithmetic Progressions Class 10 Important Questions Long Answer (4 Marks)

Question 53.
If pth, qth and rth terms of an A.P. are a, b, c respectively, then show that (a - b)r + (b - c)p+ (c - a)q = 0.
Year of Question:(2011D)

Solution:
Let A be the first term and D be the common difference of the given A.P.
pth term = A + (p - 1)D = a .(i)
qth term = A + (q - 1)D = b .(ii)
rth term = A + (r - 1)D = c . (iii)
L.H.S. = (a - b)r + (b - c)p + (c - a)q
= [A + (p - 1)D - (A + (q - 1)D)]r + [A + (q - 1)D - (A + (r - 1)D)]p + [A + (r - 1)D - (A + (p - 1)D)]q
= [(p - 1 - q + 1)D]r + [(q - 1 - r + 1)D]p + [(r - 1 - p + 1)D]q
= D[(p - q)r + (q - r)p + (r - p)q]
= D[pr - qr + qp - rp + rq - pq]
= D[0] = 0 = R.H.S.

Question 54.
The 17th term of an AP is 5 more than twice its 8th term. If the 11th term of the AP is 43, then find its nth term.
Year of Question:(2012D)

Solution:

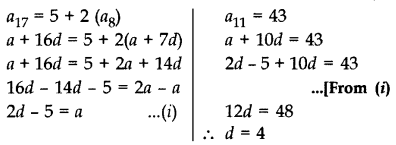
From (i),
a = 2(4) - 5 = 8 - 5 = 3
As an = a + (n - 1) d
∴ an = 3 + (n - 1) 4 = 3 + 4n - 4
an = (4n - 1)

Question 55.
The 15th term of an AP is 3 more than twice its 7th term. If the 10th term of the AP is 41, then find its nth term.
Year of Question:(2012D)

Solution:

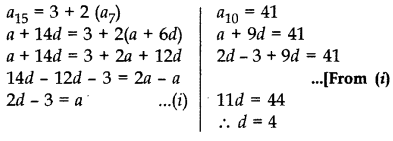
From (i),
a = 2(4) - 3
= 8 - 3 = 5
nth term = a + (n - 1) d
∴ nth term = 5 + (n - 1) 4
= 5 + 4n - 4 = (4n + 1)

Question 56.
The 16th term of an AP is 1 more than twice its 8th term. If the 12th term of the AP is 47, then find its nth term.
Year of Question:(2012D)

Solution:

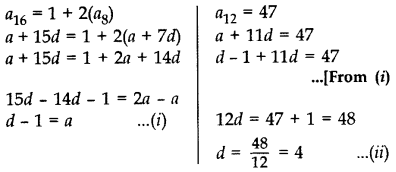
From (i) and (ii), a = 4 - 1 = 3
As nth term = a + (n - 1) d
∴ nth term = 3 + (n - 1) 4
= 3 + 4n -4 = 4n -1

Question 57.
A sum of ₹1,600 is to be used to give ten cash prizes to students of a school for their overall academic performance. If each prize is ₹20 less than its preceding prize, find the value of each of the prizes.
Year of Question:(2012OD)

Solution:
Here S10 = 1600, d = -20, n = 10
Sn = n/2 (2a + (n - 1)d]
∴ 10/2[2a + (10 - 1)(-20)] = 1600
2a - 180 = 320
2a = 320 + 180 = 500
a = 250
∴ 1st prize = a = ₹250
2nd prize = a2 = a + d = 250 + (-20) = ₹230
3rd prize = a3 = a2 + d = 230 - 20 = ₹210
4th prize = a4 = a3 + d = 210 - 20 = ₹190
5th prize = a5 = a4 + d = 190 - 20 = ₹170
6th prize = a6 = a5 + d = 170 - 20 = ₹150
7th prize = a7 = a6 + d = 150 - 20 = ₹130
8th prize = a8 = a7 + d = 130 - 20 = ₹110
9th prize = a9 = a8 + d = 110 - 20 = ₹590
10th prize = a10 = a9 + d = 90 - 20 = ₹70
= ₹ 1,600

Question 58.
Find the 60th term of the AP 8, 10, 12, ., if it has a total of 60 terms and hence find the sum of its last 10 terms.
Year of Question:(2015OD)

Solution:
a = 8, d = a2 - a1 = 10 - 8 = 2, n = 60
a60 = a + 59d = 8 + 59(2) = 126
∴ Sum of its last 10 terms = S60 - S50
= n/2(a + an) - n/2(2a + (n - 1)d)
= 60/2 (8 + a60) - 50/2 (2 × 8 + (50 - 1)2)
= 30 (8 + 126) - 25 (16 + 98)
= 4020 - 25 × 114
= 4020 - 2850 = 1170

Question 59.
An Arithmetic Progression 5, 12, 19, . has 50 terms. Find its last term. Hence find the sum of its last 15 terms.
Year of Question:(2015OD)

Solution:
Let a and d be the first term and common difference of A.P. respectively,
a = 5, d = 12 - 5 = 7, n = 50
∴ an = a + (n - 1)d
a50 = 5 + 49(7) = 5 + 343 = 348
∴ Sum of its last 15 terms = S50 - S35
= n/2(a + an) - n/2 (2a + (n - 1)d)
= 50/2 (5 + 348) - 35/2 [2(5) + (35 - 1)7]
= 25(353) - 35/2 (10 + 238)
= 8825 - 35 × 124
= 8825 - 4340 = 4485

Question 60.
If the sum of first 4 terms of an A.P. is 40 and that of first 14 terms is 280, find the sum of its first n terms.
Year of Question:(2011D)

Solution:
Sn = n/2[2a + (n - 1) d] .(i)

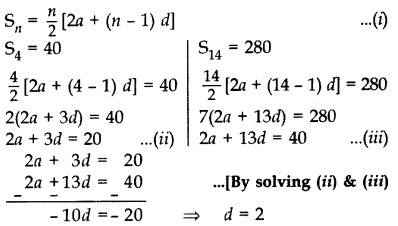
Putting the value of d = 2 in (ii), we get a = 7
∴ Sn = n/2[2(7) + (n - 1). 2]
= n/2 . 2 [7 + n - 1]
= n (n + 6) or n2 + 6n

Question 61.
The first and the last terms of an A.P. are 8 and 350 respectively. If its common difference is 9, how many terms are there and what is their sum?
Year of Question:(2011D)

Solution:
Here a = 8, an = 350, d = 9
As we know, a + (n ? 1) d = a2
∴ 8 + (n - 1) 9 = 350
(n ? 1) 9 = 350 - 8 = 342
n - 1 = 342/9 = 38
n = 38 + 1 = 39
∴ There are 39 terms.
∴ Sn = n/2(a + an)
∴S39 = 39/2 (8 + 350) = 39/2 × 358
= 39 × 179 = 6981

Question 62.
Sum of the first 20 terms of an AP is -240, and its first term is 7. Find its 24th term.
Year of Question:(2012D)

Solution:
Given: a = 7, S20 = -240
Here, Sn = n/2[2a + (n - 1)d]
∴ S20 = 20/2[2(7) + (20 - 1)d]
-240 = 10(14 + 19d)
-240/10 = 14 + 19d = -24
19d = -24 - 14 = -38
⇒ d = ?38/19 = -2 .(i)
Again, an = a + (n - 1)d
∴ a24 = 7 + (24 - 1) (-2) . [From (i)
= 7 - 46 = -39

Question 63.
Find the common difference of an A.P. whose first term is 5 and the sum of its first four terms is half the sum of the next four terms.
Year of Question:(2012OD)

Solution:
Here a = 5 . (i)
Here, a1 + a2 + a3 + a4 = 1/2 (a5 + a6 + a7 + a8)
∴ a + (a + d) + (a + 2d) + (a + 3d)
= 1/2 [(a + 4d) + (a + 5d) + (a + 6d) + (a + 780] .[an = a(n - 1)d
∴ 4a + 6d = 1/2 (4a + 22d)
8a + 12d = 4a + 22d
8a - 4a = 22d - 12d
4a = 100 ⇒ 4(5) = 10d
d = 4(5)/10=20/10 = 2 .[From (1)
∴ Common difference, d = 2

Question 64.
If the sum of the first 7 terms of an A.P. is 119 and that of the first 17 terms is 714, find the sum of its first n terms.
Year of Question:(2012OD)

Solution:
As Sn = n/2[2a + (n - 1)d]

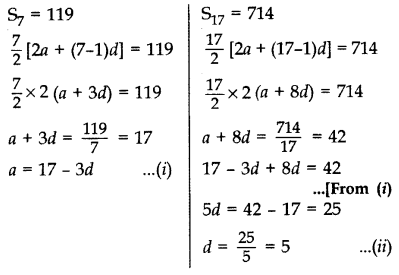
S2 = 119
From (i) and (ii), a = 17 - 3(5) = 17 - 15 = 2
∴Sn = 12[2(2) + (n - 1)5]
= n/2[4 + 5n - 5]
= n/2 (5n - 1)

Question 65.
The 24th term of an AP is twice its 10th term. Show that its 72nd term is 4 times its 15th term.
Year of Question:(2013D)

Solution:
a24 = 2 (10) . [Given
a + 23d = 2 (a +9d) [∵ an = a + (n - 1)d)
23d = 2a + 18d - a
23d - 18d = a ⇒ a = 5d .(i)
To prove: a72 = 4 (a15)

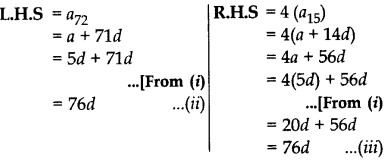
From (ii) and (iii), L.H.S = R.H.S .Hence Proved

Question 66.
Find the number of terms of the A.P. -12, -9, - 6, ., 21. If 1 is added to each term of this A.P., then find the sum of all terms of the A.P. thus obtained.
Year of Question:(2013D)

Solution:
Here a = -12, d=-9 + 12 = 3
Here, an = a + (n - 1)d = 21
∴ -12 + (n - 1).3 = 21
(n - 1).3 = 21 + 12 = 33
∴ n - 1 = 11
Total number of terms,
n = 11 + 1 = 12
New A.P. is

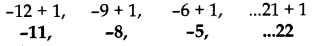
Here 1st term, a = -11
Common difference, d = -8 + 11 = 3;
Last term, an = 22; Number of terms, n= 12

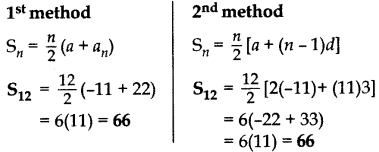
Question 67.
In an AP of 50 terms, the sum of first 10 terms is 210 and the sum of its last 15 terms is 2565. Find the AP.
Year of Question:(2014D)

Solution:
Here, n = 50,
Here, S10 = 210
= 10/2 (2a + 9d) = 210 ..[Sn = 1/2 [2a+(n - 1)2]
5(2a + 9d) = 210
2a + 9d = 210/5 = 42
⇒ 2a = 42 - 9d ⇒ a = 42-9d/2 .(i)
Now, 50 = (1 + 2 + 3 + .) + (36 + 37 + . + 50) Sum = 2565
Sum of its last 15 terms = 2565 .[Given
S50 - S35 = 2565
50/2(2a + 49d) - 35/2 (2a + 34d) = 2565
100a + 2450d - 70a - 1190d = 2565 × 2
30a + 1260d = 5130
3a + 1260 = 513 .[Dividing both sides by 10

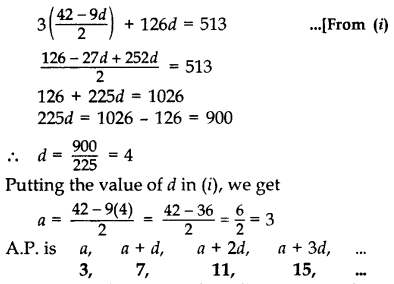
Question 68.
If the ratio of the sum of the first n terms of two A.Ps is (7n + 1): (4n + 27), then find the ratio of their 9th terms.
Year of Question:(2017OD)

Solution:

Question 69.
In a school, students decided to plant trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be double of the class in which they are studying. If there are 1 to 12 classes in the school and each class has two Sections, find how many trees were planted by the students.
Year of Question:(2014OD)

Solution:
Classes: 1 + I + II + . + XII
Sections: 2(I) + 2(II) + 2(III) + . + 2(XII)
Total no. of trees
= 2 + 4 + 6 . + 24
= (2 × 2) + (2 × 4) + (2 × 6) + . + (2 × 24)
= 4 + 8 + 12 + . + 48
:: S12 = 12/2(4 + 48) = 6(52) = 312 trees

Question 70.
Ramkali required ₹500 after 12 weeks to send her daughter to school. She saved ₹100 in the first week and increased her weekly saving by ₹20 every week. Find whether she will be able to send her daughter to school after 12 weeks.
Year of Question:(2015D)

Solution:
Money required by Ramkali for admission of her daughter = ₹2500
A.P. formed by saving
100, 120, 140, . upto 12 terms ..(i)
Let, a, d and n be the first term, common difference and number of terms respectively. Here, a = 100, d = 20, n = 12
Sn = n/2 (2a + (n - 1)d)
⇒ S12 = 12/2 (2(100) + (12 - 1)20)
S12 = 12/2 [2(100) + 11(20)] = 6[420] = ₹2520

Question 71.
The sum of first n terms of an A.P. is 5n2 + 3n. If its mth term is 168, find the value of m. Also find the 20th term of this A.P.
Year of Question:(2013D)

Solution:

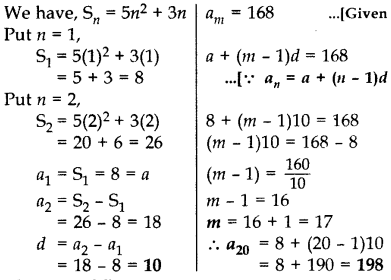
Question 72.
The sum of first m terms of an AP is 4m2 - m. If its nth term is 107, find the value of n. Also find the 21st term of this A.P.
Year of Question:(2013D)

Solution:
We have, Sm = 4m2 - m
Put m = 1,
S1 = 4(1)2 - (1)
= 4 - 1 = 3
Put m = 2,
S2 = 4(2)2 - 2
= 16 - 2 = 14
∴ a1 = S1 = 3 = a
a2 = S2 - S1 = 14 - 3 = 11
d = a2 - a1
d = 11 - 3 = 8
an = a + (n - 1)d = 107 .[Given
∴ 3+ (n - 1)8 = 107
(n - 1)8 = 107 - 3 = 104
(n - 1) = 104/8 = 13
n = 13 + 1 = 14
∴ a21 = a + 20d
= 3 + (20)8
= 3 + 160 = 163

Question 73.
The sum of first g terms of an A.P. is 63q - 3q2. If its pth term is -60, find the value of p. Also find the 11th term of this A.P.
Year of Question:(2013D)

Solution:
We have, Sq = 63q - 3q2
Put q = 1,
S7 = 63(1) - 3(1)2
= 63 - 3 = 60
Put q = 2,
S2 = 63(2) - 3(2)2
= 126 - 12 = 114
∴ a = a1 = S1 = 60
a2 = S2 - S71 = 114 - 60 = 54
d = a2 - a1 = 54 - 60 = -6
pth term = -60
a + (p - 1)d = -60
60 + (p - 1)(-6) = -60
(p - 1)(-6) = -60 - 60 = -120
(p - 1) = -120/-6 = 20
p= 20 + 1 = 21
∴ a11 = a + 10d
= 60 + 10(-6)
= 60 - 60 = 0

Question 74.
Find the sum of the first 30 positive integers divisible by 6.
Year of Question:(2011D)

Solution:
To find: 6 + 12 + 18 + . (30 terms)
Here a = 6, d = 12 - 6 = 6, n = 30
Sn = [2a + (n - 1) d]
∴ S30 = 30/2[2(6) + (30 - 1) 6]
= 15 [12 + 29(6)]
= 15 (12 + 174)
= 15 (186) = 2790

Question 75.
How many multiples of 4 lie between 10 and 250? Also find their sum.
Year of Question:(2011D)

Solution:
Multiples of 4 between 10 and 250 are:
12, 16, 20, ... 248
Here, a = 12, d = 4, an = 248
As we know, a + (n - 1) d = an
∴12 + (n - 1) 4 = 248
⇒ (n - 1) 4 = 248 - 12 = 236
n - 1 = 236/4 = 59
⇒ n = 59 + 1 = 60
∴ There are 60 terms.
Now, Sn = n/2 (a + an)
∴ S60 = [latex]60/2[/latex](12 + 248)
= 30 (260) = 7800

Question 76.
Find the sum of all multiples of 8 lying between 201 and 950.
Year of Question:(2012OD)

Solution:
To find: 208 + 216 +224 + . + 944
Here, a = 208, d = 216 - 208 = 8, an = 944
a + (n - 1)d = an
∴208 + (n - 1)8 = 944
(n - 1)8 = 944 - 208 = 736
n - 1 = 736/8 = 92
8 n = 92 + 1 = 93
Now, Sn = n/2(a1 + an)
:: S93 = 93/2 (208 + 944)
= 93/2 × 1152 = 93 × 576 = 53568

Question 77.
Find the sum of all multiples of 9 lying between 400 and 800.
Year of Question:(2012OD)

Solution:
To find: 405 + 414 + 423 + . +792
Here a = 405, d = 414 - 405 = 9, an = 792
a + (n - 1)d = an
∴ 405 + (n - 1)9 = 792
(n - 1)9 = 792 - 405 = 387
n - 1 = 387/9 = 43
∴ n = 43 + 1 = 44
As Sn = n/2(a1 + an)
∴S44 = 44/2 (405 + 792)
= 22 × 1197 = 26334

Question 78.
A thief runs with a uniform speed of 100 m/minute. After one minute a policeman runs after the thief to catch him. He goes with a speed of 100 m/minute in the first minute and increases his speed by 10 m/minute every succeeding minute. After how many minutes the policeman will catch the thief.
Year of Question:(2016D)

Solution:
Let total time ben minutes. Total distance covered by thief in n minutes
= Speed × Time
= 100 × n = 100 n metres
Total distance covered by policeman

⇒ (n - 1) (200 + 10n - 20) = 200n
⇒ (n - 1) [10n + 180) = 200n
⇒ 10n2 + 180n - 10n - 180 - 200n = 0
⇒ 10n2 - 30n - 180 = 0
⇒ n2- 3n - 18 = 0 . [Dividing both sides by 10
⇒ n2 - 6n + 3n - 18 = 0
⇒ n(n - 6) + 3(n - 6) = 0
⇒ (n + 3) (n - 6) = 0
⇒ n + 3 = 0 or n - 6 = 0
⇒ n = -3 or n = 6
But n (time) can not be negative.
∴ Time taken by policeman to catch the thief
= n - 1 = 6 - 1 = 5 minutes

Question 79.
A thief, after committing a theft, runs at a uniform speed of 50 m/minute. After 2 minutes, a policeman runs to catch him. He goes 60 m in first minute and increases his speed by 5 m/ minute every succeeding minute. After how many minutes, the policeman will catch the thief?
Year of Question:(2016D)

Solution:
Let total time be n minutes.
Total distance covered by thief in n minutes
= Speed × Time
= (50 × n) metres = 50 n metres
Total distance covered by policeman

⇒ (n - 2) (120 + 5n - 15) = 100n
⇒ (n - 2) [5n + 105) = 100n
⇒ 5n2 + 105n - 10n - 210 - 100n = 0
⇒ 5n2 - 5n - 210 = 0
⇒ n2 - n - 42 = 0 .[Dividing both sides by 5
⇒ n2 - 7n + 6n - 42 = 0
⇒ n(n - 7) + 6(n - 7) = 0
⇒ (n - 7) (n + 6) = 0
⇒ n - 7 = 0 or n + 6 = 0
⇒ n = 7 or n = -6 (reject)
But n (time) can not be negative.
∴ Time taken by policeman to catch the thief
= n - 2 = 7 - 2 = 5 minutes

Question 80.
The houses in a row are numbered conse cutively from 1 to 49. Show that there exists a value of X such that sum of numbers of houses preceding the house numbered X is equal to sum of the numbers of houses following X.
Year of Question:(2016OD)

Solution:
Here the A.P. is 1, 2, 3, .., 49
Here a = 1, d = 1, an = 49

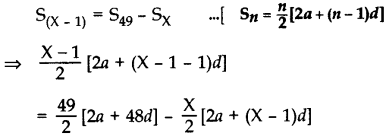
Now,
⇒ (X - 1)2 (2 + (X - 2)) = 49(2 + 48) - X[2 + (x - 1)]
⇒ (X - 1). X = 2,450 - X(X + 1)
⇒ x2 - X = 2,450 - X2- X
⇒ X2 - X + X2 + X = 2,450
⇒ 2X2 = 2,450
⇒ X2 = 1,225
∴ X = +√1,225 = 35 .[X can not be -ve

Question 81.
Find the sum of n terms of the series (4-1/n)+(4-2/n)+(4-3/n)+...
Year of Question:(2017D)

Solution:
First term, a = 4 - 1/n

Question Papers / Notes Download

Videos